Sobre los Test de primalidad I

Un test de primalidad es un criterio, para determinar si un número n, es primo o no, es decir se puede descomponer en otros o no.

Si n para el test de primalidad, entonces “puede” ser primo, en caso de que no lo pase, entendemos que es un número compuesto.

Hay un problema aún mayor, que aplicar el test de primalidad a un entero grande,  consiste en encontrar los factores primos de n, computacionalmente es más costoso este problema en el caso de que en número no supere el test de primalidad.

 

La seguridad del sistema de encriptación RSA, está basado en la asunción de que, es más fácil encontrar dos números primos p y q, tal que n = p x q, que buscar los dos factores de n.

A continuación se describen varios test de primalidad.

 Hasta 1819, se creía que un número mayor de 2 era primo, si el módulo de (2^n)/n era 2, pero la hipótesis falló para 341=11 x 31, y  mod(2^341,341)=2, por lo que se desechó dicho criterio.

De todas formas y aunque no es de mucha utilidad os dejo en código de una función en MatlLab que realiza dicha comprobación.

 function [] = esprimo(numero)
%Comprueba si un número es primo hasta el 341
%
    if numero>=341
       fprintf('El numero es mayor de 341 \n')
       fprintf('Fuera de rango \n')
       return
    end

    if mod(2.^numero,numero)==2 || numero==2
       resultado='numero es primo';
    else
       resultado='numero compuesto';
    end
  
sprintf('el numero es %s \n ',resultado)

end

 

Uno de los algoritmos más elementales es del de dividir el número que queremos comprobar por los impares inferiores (descartando los numeros pares que no son primos)

Sea n un número entero grande, y supongamos que queremos determinar, si este número es primo o no.

El más simple de los test de primalidad es el de la prueba de la división, consiste en que tenemos un entero impar m y vemos si divide o no a n, si n ≠ 1, n  y m|n ( m divide a n), entonces n es compuesto, en otro caso n pasa el test de primalidad, de la prueba de la división por m, el siguiente paso es seleccionar más y más pruebas de división , sabemos que n es primo cuando m alcanza a (n^1/2) , este método consume mucho tiempo en probar que  n es o no primo, hay otros métodos mucho más rápidos que comentaremos en próximos post.

Otro sería el de la criba de Eratóstenes

Sea n el número del que queremos conocer su primalidad, el procedimiento es:

• Crear una lista con los números naturales de 1 hasta n.
• Sea p el primer número natural no marcado, inicialmente p=2, marcar todos los múltiplos de p.
• Si p≤√ n  entonces seleccionar el siguiente p y volver al segundo paso. En caso contrario, parar.

Eratóstenes de Cirene

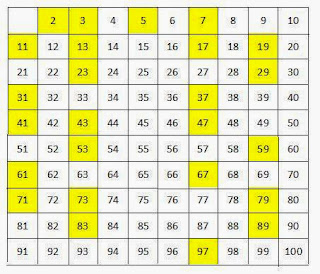
 En la siguiente imagen se muestra la criba hasta el número 100, en amarillo evidentemento los números primos.

 

Como se puede comprobar se basan en el mismo principio, y son costosos computacionalmente para números muy grandes por lo que exploraremos otros métodos.

 

Evidentemente continuaremos...